<IMG style="CURSOR: pointer" onclick="self.parent.InsertSymbol('




☆ ~ 幻 星 ~ ☆ 寫到:
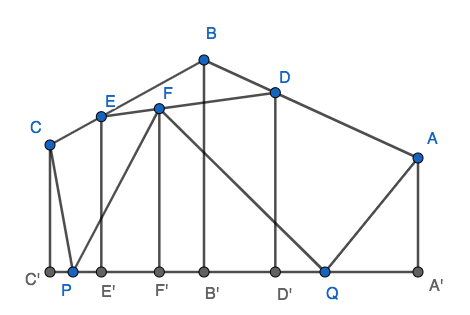
重點:三角形面積比 = 高的比
所以假設A, B, C, D, E, F到直線PQ的垂足為A', B', C', D', E', F'
則AA':BB':CC'=a:b:c
看梯形AA'B'B及截線DD',AA':BB':DD'=a:b:(a+2b)/3
看梯形CC'B'B及截線EE',CC':BB':EE'=c:b:(b+2c)/3
看梯形DD'E'E及截線FF',DD':EE':FF'=(a+2b)/3:(b+2c)/3:(a+4b+4c)/9
所以答案就是(a+4b+4c)/9
