eaglle �g��:�q��7���n���Xg�����ͪ��0, �]�\���~: g �ͪ��0, ln g �ͪ��t�L���j, �٬O���i�� g lng�����w��
���w�즡���K, �O�䬰a, �h
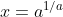
��x�ݰ�a�����, �i����̤j�ȵo�ͦba=e, �]�N�O
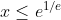
��
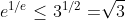
�ҥH, �b���K�����]�U, x���i��O����, �������p��ڸ�3,
�ҥH, x=2,
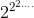
���㤣���K
�Ҩ����O�C�@�س�²�檺�ץ��覡�A�O���]a ������0�ɡA�i���� x���W���C
�Ya=0, �۵Mf_n �L�W���o���C
�ڪ����~�b�� lim g_n ln g_{n+1}, �����t�@���C�Y�O g_n ln g_n, �h g_n �ͪ��0�ɡA�� L��Hôpital��s Rule, �����ȷ��O0�C���b�������ɡA�O���@�Ǥߵ�A���H���t�@���S���Y�A�]�S�A�T�{�U��x�����p�A�Q���̤@���ݯ}�A�P�«����C
���L�A��� f(x)=x^(1/x) ���̤j�ȡA���� ���w��ƭ�b=f(x), �i���ӸѡA���n�p��O�ҭ�po x^(x^(x... �u�|���V�䤤�@�ӸѡA�ݨӭ�po�l�ͥX�����D���Z���쪺�C
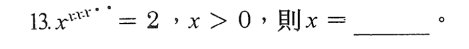
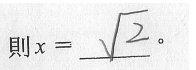

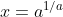
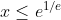
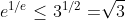
���㤣���K
