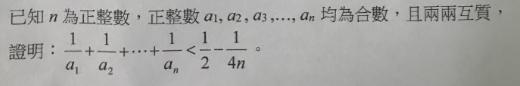[國中]一題證明

第1頁(共1頁)
因為 a1, a2, a3, ..., an 均為合數(合成數),且兩兩互質,
所以
1/a1 + 1/a2 + 1/a3 + ... + 1/an
≦ 1/2² + 1/3² + 1/5² + 1/7² + 1/11² + ... + 1/pn²
( 2, 3, 5, 7, 11, ..., pn 為前 n 個質數 )
< 1/2² + 1/3² + 1/5² + 1/7² + 1/9² + ... + 1/(2n - 1)²
( 3, 5, 7, 9, ..., 2n - 1 為第 2 個到第 n 個正奇數 )
< 1/2² + 1/(2*4) + 1/(4*6) + 1/(6*8) + 1/(8*10) + ... + 1/[(2n - 2)(2n)]
( 因為 (2k - 1)² = 4k² - 4k + 1 = (2k - 2)(2k) + 1 > (2k - 2)(2k),
所以 1/(2k - 1)² < 1/[(2k - 2)(2k)] for k = 2, 3, 4, ..., n )
= 1/2² + (1/2 - 1/4)/2 + (1/4 - 1/6)/2 + (1/6 - 1/8)/2 + (1/8 - 1/10)/2 + ... + [1/(2n - 2) - 1/(2n)]/2
= 1/2² + (1/2
= 1/2² + (1/2)/2 - [1/(2n)]/2
= 1/4 + 1/4 - 1/(4n)
= 1/2 - 1/(4n)
-
benice - 專 家

- 文章: 269
- 註冊時間: 2010-02-08
第1頁(共1頁)