�D�Y�ƽƤ�{��z^2-2(1+I)z-5-10i=0 z�Ѭ��H
�D�p��L�{����4+3i -2-i
[����]2-3�h������{��

��1��(�@1��)
z² - 2(1 + i)z - 5 - 10i = 0
z² - 2(1 + i)z - (5 + 10i) = 0
�ѤG����{���������ѡA�o
z
= {2(1 + i) �� ��[4(1 + i)² + 4(5 + 10i)]} / 2
= (1 + i) �� ��[(1 + i)² + (5 + 10i)]
= (1 + i) �� ��[2i + 5 + 10i]
= (1 + i) �� ��[5 + 12i]
= (1 + i) �� ��[3² + 2*3*2i + (2i)²]
= (1 + i) �� ��[(3 + 2i)²]
= (1 + i) �� (3 + 2i)
= (1 + i) + (3 + 2i) �� (1 + i) - (3 + 2i)
= 4 + 3i �� -2 - i ��
�Ϊ̪����ΰt��k�G
z² - 2(1 + i)z - 5 - 10i = 0
z² - 2(1 + i)z + (1 + i)² = 5 + 10i + (1 + i)²
[z - (1 + i)]² = 5 + 10i + 2i
[z - (1 + i)]² = 5 + 12i
[z - (1 + i)]² = 3² + 2*3*2i + (2i)²
[z - (1 + i)]² = (3 + 2i)²
z - (1 + i) = ��(3 + 2i)
z = 1 + i �� (3 + 2i) = 4 + 3i �� -2 - i ��
-
benice - �M�@�a

- �峹: 269
- ���U�ɶ�: 2010-02-08
(�t��)
���G
1. ����k�p����c���A�ȨѰѦҡC
2. ���L�k�D�X���T�Ѯ�(�Ҧp�����h������{��)�A�i�Q�Φ���kø�ϱo�����ѡC
�O z = x + yi, x, y ����ơC
�h
(x + yi)² - 2(1 + i)(x + yi) - 5 - 10i = 0
(x² - y² + 2xyi) - 2[x - y + (x + y)i] - 5 - 10i = 0
(x² - y² - 2x + 2y - 5) + 2(xy - x - y - 5)i = 0
�ҥH
��
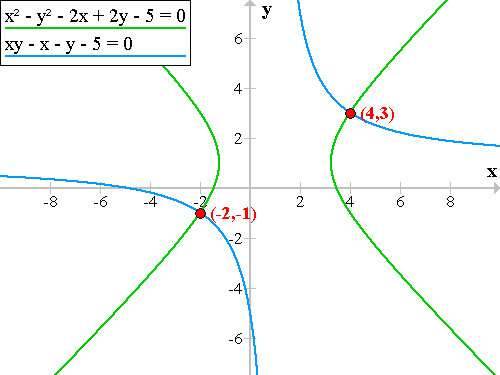
�xx² - y² - 2x + 2y - 5 = 0
�xxy - x - y - 5 = 0 (�аѦҤU�����ϧ�)
��
�t��o
��
�x(x² - 2x + 1) - (y² - 2y + 1) - 5 = 0
�x(x - 1)(y - 1) - 6 = 0
��
��
�x(x - 1)² - (y - 1)² = 5
�x(x - 1)(y - 1) = 6
��
�O
a = x - 1
b = y - 1
�o
��
�xa² - b² = 5 ...... (1)
�xab = 6 ...... (2)
��
�� (2) �o
b = 6/a ...... (3)
�N (3) �N�J (1) �o
a² - (6/a)² = 5
(a²)² - 5a² - 36 = 0
(a² - 9)(a² + 4) = 0
a² = 9
a = ��3
�N a = ��3 �N�J (3) �o
b = ��2
�ҥH
x = a + 1 = (3 + 1) �� (-3 +1) = 4 �� -2
y = b + 1 = (2 + 1) �� (-2 +1) = 3 �� -1
�]���A���{�����Ѭ� 4 + 3i �� -2 - i�C ��
�ѦҹϡG
-
benice - �M�@�a

- �峹: 269
- ���U�ɶ�: 2010-02-08
��1��(�@1��)