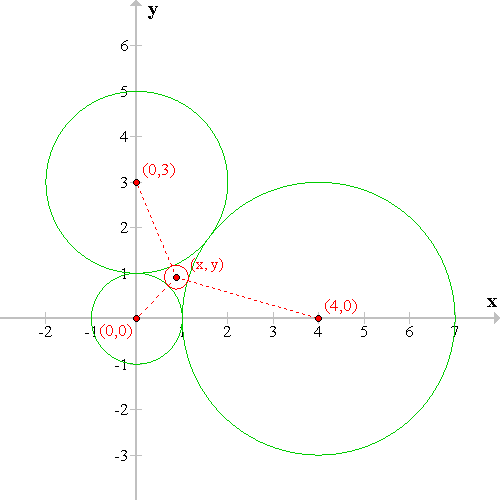由 benice 於 星期三 十月 26, 2016 6:00 pm
由 benice 於 星期三 十月 26, 2016 6:00 pm
因為三個大圓的圓心距 1+2, 1+3, 2+3 滿足 (1+2)² + (1+3)² = (2+3)²,
恰好為直角三角形的三邊,所以可以將圖形適當旋轉,得到以下圖形:
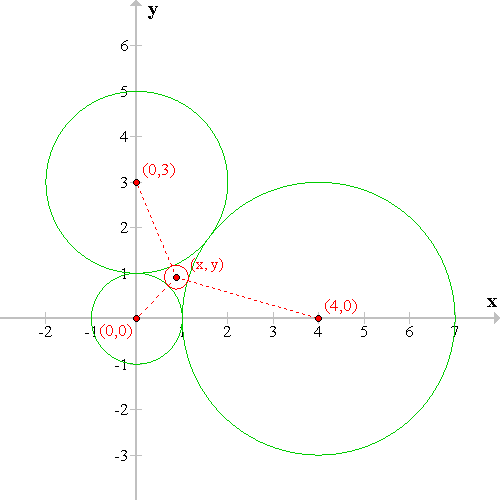
設上圖中小圓的圓心在 (x,y),半徑為 r,則
(x - 0)² + (y - 0)² = (1 + r)²
(x - 4)² + (y - 0)² = (3 + r)²
(x - 0)² + (y - 3)² = (2 + r)²
即
x² + y² = (1 + r)² ...... (1)
(x - 4)² + y² = (3 + r)² ...... (2)
x² + (y - 3)² = (2 + r)² ...... (3)
(2) - (1) 得
(x - 4)² - x² = (3 + r)² - (1 + r)²
(2x - 4)(-4) = (2r + 4)(2) ( By 平方差公式 a² - b² = (a + b)(a - b) )
(4 - 2x)(4) = (r + 2)(4)
4 - 2x = r + 2
2x = 2 - r
x = 1 - r/2 ...... (4)
(3) - (1) 得
(y - 3)² - y² = (2 + r)² - (1 + r)²
(2y - 3)(-3) = (2r + 3)(1)
6y - 9 = -2r - 3
6y = 6 - 2r
y = 1 - r/3 ...... (5)
將 (4), (5) 代入 (1) 得
(1 - r/2)² + (1 - r/3)² = (1 + r)²
r²/4 - r + 1 + r²/9 - 2r/3 + 1 = r² + 2r + 1
r²/4 + 1 + r²/9 - 2r/3 = r² + 3r
9r² + 36 + 4r² - 24r = 36r² + 108r ( 上式同乘 36 )
23r² + 132r - 36 = 0
(r + 6)(23r - 6) = 0
r = 6/23 (Ans.) 或 r = -6 (負根不合)
r = 6/23 代入 (4), (5) 得
x = 1 - 3/23 = 20/23
y = 1 - 2/23 = 21/23 ■