1.請問dim(V)=rank(T)+Nullity(T) 是指什麼?怎麼證明?2.A=2*2矩陣 0 1 0 0 rank(A)=1是為什麼?怎麼計算的?
3.請問以下是非題敘述要如何解釋(說明)
(g) Linear operaters on infinite dimentional vector spaces never have eigenvalues.(h)An n*n matrix A with entries from a field F is similar to a diagonal matrix if and only if there is a basis for F^n consisting of eigenvectors of A. (j) Similar matrixes always have the same eigenvectors.4.為何微分是線性函數?5.O中間加一直線(數學符號)是什麼意思?怎麼運用? (A->La(x)兩個中間的數學符號)感謝
[大學] 線性代數問題

第1頁(共1頁)
1. N(T) 是指那些T作用下去會得到0的V中的向量 =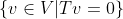
R(T)是指T作用在V上的所有的結果 =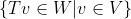
其實, 你需要一個圖來理解:

現在, 為R找一個basis: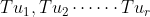
換言之, 我們假設R是r維的;
再為N找一個basis: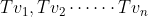
也就是假設N的維數是n
接下來, 我們可以証明: 這些v's 和這些u's合起來, 一定會是V的basis , (這部份就請你查書了)
這樣, 使等於証明了V的維數是r+n,
總之, N和R的維數和, 恰等 於V的維數, 這件事情可以這樣看 (但不是証明, 証明在上面):
原來V的維數是某數, 但T會將其中的n維(即N的維數) 殺掉 (映至0), 而映出來的有r維(即R的維數),
換言之, 某數-n=r, 所以某數就等於n+r了啊
(正式的証明書上都有, 但上面的圖, 和這個看法, 是一般書上不會有的)
查書如有不明白的, 再提出來不要客氣
R(T)是指T作用在V上的所有的結果 =
其實, 你需要一個圖來理解:

現在, 為R找一個basis:
換言之, 我們假設R是r維的;
再為N找一個basis:
也就是假設N的維數是n
接下來, 我們可以証明: 這些v's 和這些u's合起來, 一定會是V的basis , (這部份就請你查書了)
這樣, 使等於証明了V的維數是r+n,
總之, N和R的維數和, 恰等 於V的維數, 這件事情可以這樣看 (但不是証明, 証明在上面):
原來V的維數是某數, 但T會將其中的n維(即N的維數) 殺掉 (映至0), 而映出來的有r維(即R的維數),
換言之, 某數-n=r, 所以某數就等於n+r了啊
(正式的証明書上都有, 但上面的圖, 和這個看法, 是一般書上不會有的)
查書如有不明白的, 再提出來不要客氣
-
eaglle - 研究生

- 文章: 114
- 註冊時間: 2014-10-21
3. 先說答案, 理由再補:
Linear operaters on infinite dimentional vector spaces never have eigenvalues.----錯
(h)An n*n matrix A with entries from a field F is similar to a diagonal matrix if and only if there is a basis for F^n consisting of eigenvectors of A.------正確
(j) Similar matrixes always have the same eigenvectors.----錯
Linear operaters on infinite dimentional vector spaces never have eigenvalues.----錯
(h)An n*n matrix A with entries from a field F is similar to a diagonal matrix if and only if there is a basis for F^n consisting of eigenvectors of A.------正確
(j) Similar matrixes always have the same eigenvectors.----錯
-
eaglle - 研究生

- 文章: 114
- 註冊時間: 2014-10-21
補上3. 的理由:
Linear operaters on infinite dimentional vector spaces never have eigenvalues.----錯
反例: 例如D為微分算子, vector space ={所有可微分函數},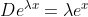
所以, 任何實數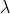 都是 eigen value
都是 eigen value
(h)An n*n matrix A with entries from a field F is similar to a diagonal matrix if and only if there is a basis for F^n consisting of eigenvectors of A.------正確
(j) Similar matrixes always have the same eigenvectors.----錯
如果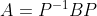 , 而
, 而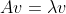
則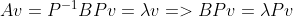
所以, 若v是A的eigen vector, 則 Pv 是B的eigen vector; A的eigen vector 和B的不一樣
Linear operaters on infinite dimentional vector spaces never have eigenvalues.----錯
反例: 例如D為微分算子, vector space ={所有可微分函數},
所以, 任何實數
(h)An n*n matrix A with entries from a field F is similar to a diagonal matrix if and only if there is a basis for F^n consisting of eigenvectors of A.------正確
(j) Similar matrixes always have the same eigenvectors.----錯
如果
則
所以, 若v是A的eigen vector, 則 Pv 是B的eigen vector; A的eigen vector 和B的不一樣
-
eaglle - 研究生

- 文章: 114
- 註冊時間: 2014-10-21
第1頁(共1頁)