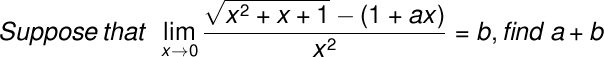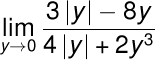1.
√(x² + x + 1) - (1 + ax)
lim ────────────── (0/0 不定型)
x→0 x²
(2x + 1)/[2√(x² + x + 1)] - a
= lim ──────────────── (by L'Hospital's Rule)
x→0 2x
如果 a = 1/2,則上式為 0/0 不定型,極限有可能存在。
如果 a < 1/2,則上式的左極限為 -∞,右極限為 ∞,故極限不存在。
如果 a > 1/2,則上式的左極限為 ∞,右極限為 -∞,故極限不存在。
(2x + 1)/[2√(x² + x + 1)] - 1/2
lim ─────────────────
x→0 2x
2x + 1 - √(x² + x + 1)
= lim ───────────── (0/0 不定型)
x→0 4x√(x² + x + 1)
2 - (2x + 1)/[2√(x² + x + 1)]
= lim ─────────────────────── (by L'Hospital's Rule)
x→0 4√(x² + x + 1) + 2x(2x + 1)/√(x² + x + 1)
2 - 1/2
= ─────
4
= 3/8
因此 a = 1/2,b = 3/8,a + b = 7/8。 ■
2.
y > 0 時
(3|y| - 8y) / (4|y| + 2y³)
= (3y - 8y) / (4y + 2y³)
= -5 / (4 + 2y²)
→ -5/4 as y → 0+
y < 0 時
(3|y| - 8y) / (4|y| + 2y³)
= (-3y - 8y) / (-4y + 2y³)
= -11 / (-4 + 2y²)
→ 11/4 as y → 0-
左極限≠右極限,故極限不存在。 ■
─────────────────────────────────────
My Gallery:
benice equation (benice 方程式)