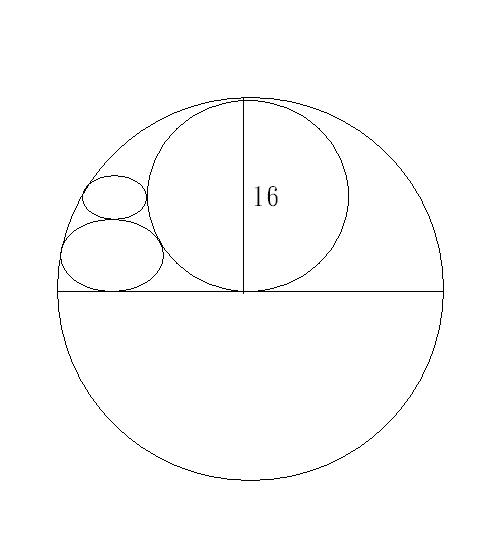
 求小圓半徑
求小圓半徑[國中]圖形難題

第1頁(共1頁)
Re: [國中]圖形難題
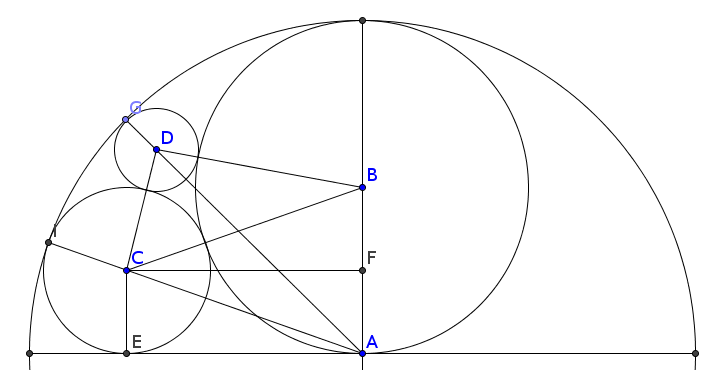
令 半徑 AB = b (B為圓心), 中圓(C為圓心)的半徑 CE = c, 小圓(D為圓心) 的半徑 = d
則 BC = b+c, BD=b+d, CD=c+d, 圓A的半徑=2b
因為圓C與圓A內切, 所以 所以ACI共線, AC = AI - CI = 2b - c
同理, 圓D與圓A內切, 所以 AD = AG - DG = 2b -d
輔助線CF⊥AB, CE⊥AE, 所以 AF=CE=c
ΔBCF 與 ΔACF為直角三角形, 所以
(b+c)2 - (b-c)2 = (2b-c)2 - c2
4bc = 4b2 - 4bc
b = 2c
所以 AC = 3c = BC, CF = 2√2c
令 角EAC = θ, 角CAD = α, 角DAB = β
則 θ+α+β = 90° , sin θ = 1/3 = cos (α+β)
對ΔCAD而言,
cos α = (AC2 + AD2 - CD2)/2/AC/AD = [(4c-d)2 + (3c)2 - (c+d)2]/2/(4c-d)/(3c) = (12c-5d)/3/(4c-d)
對ΔDAB而言,
cos β = (AD2 + AB2 - BD2)/2/AD/AB = [(4c-d)2 + (2c)2 - (2c+d)2]/2/(4c-d)/(2c) = (4c-3d)/(4c-d)
三角恆等式:
cos(α+β) = cos(α) cos(β) - sin(α) sin(β)
所以,
[sin(α) sin(β)]2 = [cos(α) cos(β) - cos(α+β)]2 = [cos(α) cos(β) - 1/3]2
[1-cos2(α)][1-cos2(β)] = cos2(α) cos2(β) - 2cos(α) cos(β)/3 + 1/9
1 - cos2(α) -cos2(β) = 1/9 - 2cos(α) cos(β)/3
8(4c-d)2 = (12c-5d)2 + 9(4c-3d)2 - 2(12c-5d)(4c-3d)
17d2 - 40cd + 16c2 = 0
d/c = (20-8√2)/17 (≈0.51096)
註: 看不出有其它更簡單的方法可解此題, 並不難解(用畢式定理即可), 只是要有耐心.
-
lskuo - 專 家

- 文章: 278
- 註冊時間: 2010-11-10
第1頁(共1頁)
