
[國中] 數學科試題

第1頁(共1頁)
令
x = a + b ...... (1)
y = a - b ...... (2)
因為 a > b > 0,所以 x > y > 0。
又因為 a, b 為正整數,所以 x, y 也是正整數。
用加減消去法解方程組 (1), (2) 可得:
a = (x + y)/2 ...... (3)
b = (x - y)/2 ...... (4)
以下將題目所給的 a, b 的關係式轉換成 x, y 的關係式:
4(a² + ab + b²) = 49(a + b)
4{[(x + y)/2]² + [(x + y)/2][(x - y)/2] + [(x - y)/2]²} = 49[(x + y)/2 + (x - y)/2]
(x + y)² + (x + y)(x - y) + (x - y)² = 49x
2x² + 2y² + x² - y² = 49x
3x² + y² = 49x
y² = 49x - 3x²
y = √(49x - 3x²) = √[x(49 - 3x)]
因為上式的根號內部需大於零,
所以 49 > 3x,即 x < 49/3 = 16 + 1/3,
因此 x ≦ 16。
因為 x > y,
所以 x² > y²,
x² > x(49 - 3x),
x > 49 - 3x, (註:因為 x > 0,所以不等式可同除 x)
4x > 49,
x > 49/4 = 12 + 1/4,
因此 x ≧ 13。
x | y | y 為整數?
---------------------------------
13 | √(13×10) | 否
---------------------------------
14 | √(14×7) | 否
---------------------------------
15 | √(15×4) | 否
---------------------------------
16 | √(16×1) | 4
---------------------------------
所以 x = 16, y = 4,將其代入 (3), (4) 得
a = (16 + 4)/2 = 10
b = (16 - 4)/2 = 6 ■
參考圖:
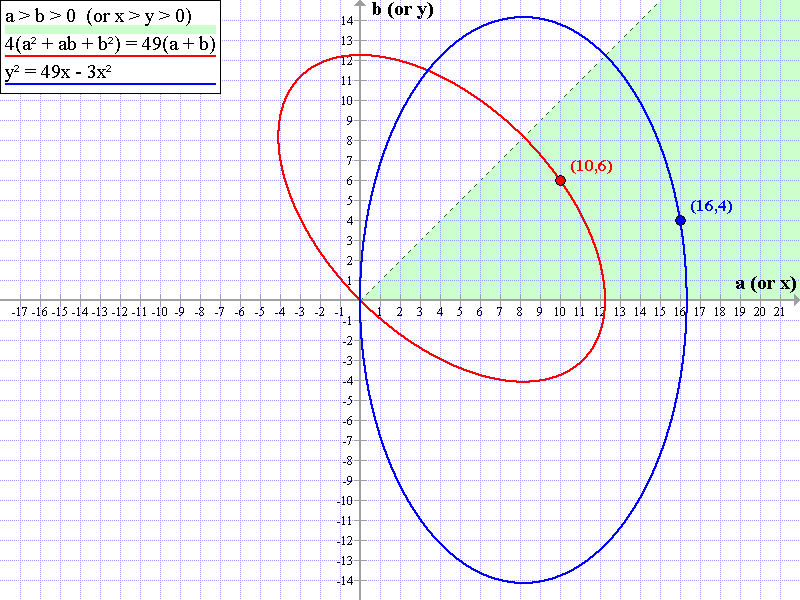
上圖同時顯示 a-b 座標系與 x-y 座標系:
不等式 a > b > 0, 方程式 4(a² + ab + b²) = 49(a + b), 紅點 (10, 6) 為 a-b 座標系的圖;
不等式 x > y > 0, 方程式 y² = 49x - 3x², 藍點 (16, 4) 為 x-y 座標系的圖。
-
benice - 專 家

- 文章: 269
- 註冊時間: 2010-02-08
另解 (想法比較簡單,但數字計算比較繁雜):
4(a² + ab + b²) = 49(a + b)
4b² + (4a - 49)b + (4a - 49)a = 0
將上式視為 b 的二次方程式,
則公式解的判別式
= (4a - 49)² - 4*4*(4a - 49)a
= (4a - 49)(4a - 49 - 16a)
= (4a - 49)(-12a - 49)
= (49 - 4a)(12a + 49)
因為 b 為正整數,當然也是實數,
所以判別式 (49 - 4a)(12a + 49) ≧ 0,
49 - 4a ≧ 0, (註:因為 12a + 49 > 0,所以不等式可同除 12a + 49)
4a - 49 ≦ 0,
a ≦ 49/4 = 12 + 1/4,
因此 a ≦ 12。
由公式解求得
b = { 49 - 4a + √[(49 - 4a)(12a + 49)] } / 8
(註:因為 (49 - 4a)² < (49 - 4a)(12a + 49),所以公式解的另一解小於零,不合)
因為 a > b,
所以 8a > 8b,
所以 8a > 49 - 4a + √[(49 - 4a)(12a + 49)],
12a - 49 > √[(49 - 4a)(12a + 49)],
(12a - 49)² > (49 - 4a)(12a + 49),
12²a² - 2*12*49a + 49² > -4*12a² + (49*12 - 4*49)a + 49²,
12(12 + 4)a² > 32*49a,
3(16)a > 8*49, (註:因為 a > 0,所以不等式可同除 a)
6a > 49,
a > 49/6 = 8 + 1/6,
因此 a ≧ 9。
a | 判別式是否為完全平方數?
--------------------------------------------------------------------
9 | (49 - 36)(108 + 49) = 13*157 (157 為質數), 否
--------------------------------------------------------------------
10 | (49 - 40)(120 + 49) = 9*169 = 3²*13² = 39², 是
--------------------------------------------------------------------
11 | (49 - 44)(132 + 49) = 5*181 (181 為質數), 否
--------------------------------------------------------------------
12 | (49 - 48)(144 + 49) = 193 (193 為質數), 否
--------------------------------------------------------------------
所以只有在 a = 10 時,b 才可能為整數。
a = 10 時,b = (49 - 4*10 + √39²) / 8 = 48 / 8 = 6 也是整數。
故數對 (a, b) 只有唯一解 (10, 6)。 ■
-
benice - 專 家

- 文章: 269
- 註冊時間: 2010-02-08
第1頁(共1頁)
