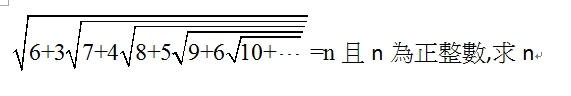
[國中]一個根式內無限

第1頁(共1頁)
題目怪怪的!
(√6 + 2√7 + 3√8 + 4√9 + 5√10 + …) ≦ 原式 ≦ (√7 + 3√8 + 4√9 + 5√10 + 6√11 + …)
而
(√6 + 2√7 + 3√8 + 4√9 + 5√10 + …) = 4
(√7 + 3√8 + 4√9 + 5√10 + 6√11 + …) = 5
所以
4 ≦ 原式 ≦ 5。
原式的近似值約為 4.862096497794835 (請參考下圖)。
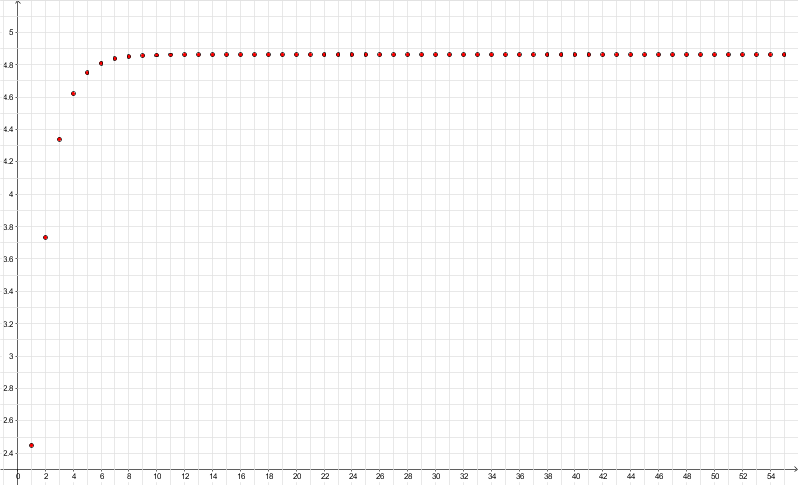
上圖中的紅點代表 (n, f(n)), n = 1 ~ 55。
f(n) 定義如下:
f(1) = sqrt(6)
f(2) = sqrt(6 + 3*sqrt(7))
f(3) = sqrt(6 + 3*sqrt(7 + 4*sqrt(8)))
f(4) = sqrt(6 + 3*sqrt(7 + 4*sqrt(8 + 5*sqrt(9))))
f(5) = sqrt(6 + 3*sqrt(7 + 4*sqrt(8 + 5*sqrt(9 + 6*sqrt(10)))))
其餘依此類推。
-
benice - 專 家

- 文章: 269
- 註冊時間: 2010-02-08
訪客 寫到:(√6 + 2√7 + 3√8 + 4√9 + 5√10 + …) = 4
(√7 + 3√8 + 4√9 + 5√10 + 6√11 + …) = 5
請教等於4等於5這兩式怎麼算出來的?
使用 Ramanujan's infinite radicals
x + n + a = √ax + (n+a)² + x√a(x+n) + (n+a)² + (x+n)√a(x+2n) + (n+a)² + (x+2n)√a(x+3n) + (n+a)² + (x+3n)√…
代入 x = 2, n = 1, a = 1 可得
2 + 1 + 1 = √6 + 2√7 + 3√8 + 4√9 + 5√10 + …
代入 x = 3, n = 1, a = 1 可得
3 + 1 + 1 = √7 + 3√8 + 4√9 + 5√10 + 6√11 + …
-
benice - 專 家

- 文章: 269
- 註冊時間: 2010-02-08
第1頁(共1頁)