由 benice 於 星期五 八月 19, 2016 8:40 am
由 benice 於 星期五 八月 19, 2016 8:40 am
旋轉公式:
某點原先位於座標 (x,y),以原點為轉軸,逆時針旋轉θ弧度後,該點位置變成座標 (x',y'),則:
x' = x cosθ - y sinθ
y' = x sinθ + y cosθ
------------------------------------------------------------------------------------------------------------------
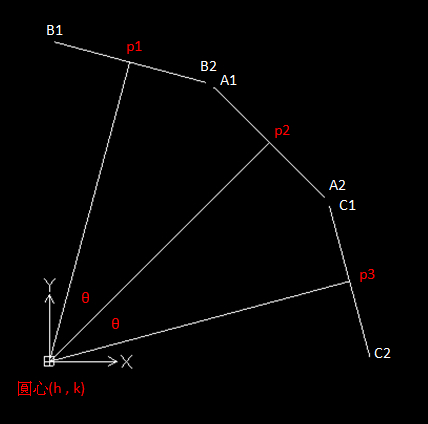
假設 p1, p2, p3 分別為 B1 與 B2, A1 與 A2, C1 與 C2 的中點,則:
p1 = (B1 + B2)/2 = ((4.904 + 141.506)/2, (291.506 + 254.904)/2) = (73.205, 273.205)
p2 = (A1 + A2)/2 = ((150 + 250)/2, (250 + 150)/2) = (200, 200)
p3 = (C1 + C2)/2 = ((254.904 + 291.506)/2, (141.506 + 4.904)/2) = (273.205, 73.205)
設圓心座標為 (a,b)。
p1, p2, p3 對 (a,b) 的相對座標分別為
p1' = (73.205 - a, 273.205 - b)
p2' = (200 - a, 200 - b)
p3' = (273.205 - a, 73.205 - b)
(1) 由『p3 以 (a,b) 為轉軸,逆時針旋轉 30° 後的點為 p2』,求 a, b 的值:
『p3 以 (a,b) 為轉軸,逆時針旋轉 30° 後的點為 p2』
相當於
『p3' 以 (0,0) 為轉軸,逆時針旋轉 30° 後的點為 p2'』
由旋轉公式,
200 - a = (273.205 - a)cos(30°) - (73.205 - b)sin(30°)
200 - b = (273.205 - a)sin(30°) + (73.205 - b)cos(30°)
200 - a = (273.205 - a)(sqrt(3)/2) - (73.205 - b)(1/2)
200 - b = (273.205 - a)(1/2) + (73.205 - b)(sqrt(3)/2)
400 - 2a = sqrt(3)(273.205 - a) - 73.205 + b
400 - 2b = 273.205 - a + sqrt(3)(73.205 - b)
以上方程組的 Mathematica 計算結果:
In[1]:= NSolve[{400 - 2a == Sqrt[3] (273.205 - a) - 73.205 + b,
400 - 2b == 273.205 - a + Sqrt[3] (73.205 - b)}, {a,b}]
Out[1]= {{a -> -0.000191073, b -> 0.000110316}}
所以,(a,b) ≒ (-0.000191073, 0.000110316)。
(2) 由『p2 以 (a,b) 為轉軸,逆時針旋轉 30° 後的點為 p1』,求 a, b 的值:
可以仿照 (1),求得
(a,b) ≒ (0.000110316, -0.000191073)。
或者由對稱性求得:
觀察 p1 與 p3 的座標值 (73.205, 273.205) 與 (273.205, 73.205),
得知 p1 的 x, y 座標恰等於 p3 的 y, x 座標,
所以 p1, p3 對稱於對角線 y = x。
而 p2 座標為 (200, 200),恰好落在對角線 y = x 上,
因此,所求的 a, b 值恰為 (1) 求得的 b, a 值。