老師在黑板上寫了23個整數,讓聖友計算它們的平均數(保留三位小數)。聖友計算出的答案是16.654。老師說"除最後一位數字外,其他都對了。"請問:正確的平均數是多少?
答:16.652
想了很久,總覺得條件不足,不知是哪裡有問題,再麻煩各位幫忙一下,謝謝~~
[國小]數學競賽題目

第1頁(共1頁)
先把2016這個數字想像成2016個1塊錢好了
把這19個數想像成19個戶頭,首先給每1個戶頭不一樣的金額,必須使用掉190元
}{2}=190)
接下來剩下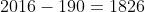 元
元
平均分配到19個戶頭,每個戶頭96元,多出2元
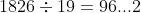
多出來2元分給最大的2個戶頭
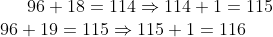
所以最大數-最小數的最小值=(96+20)-(96+1)=19
把這19個數想像成19個戶頭,首先給每1個戶頭不一樣的金額,必須使用掉190元
接下來剩下
平均分配到19個戶頭,每個戶頭96元,多出2元
多出來2元分給最大的2個戶頭
所以最大數-最小數的最小值=(96+20)-(96+1)=19
-

J+W - 版 主

- 文章: 2162
- 註冊時間: 2003-12-30
設五個連續整數由大到小為A,B,C,D,E
其中A-E=4,A-D=3,A-C=2,A-B=1
B-E=3,B-D=2,B-C=1
C-D=1
其次33=10+11+12≦任意三個兩位數和≦99+98+97=294
要滿足題意,第一組的三個兩位數和第二組的三個兩位數至少有一個數字,最多有2個數字是相同的
若有兩個數字是相同的,兩組數字和所能製造出來最大的差是4,最小的差是1
若有一個數字是相同的,兩組數字和所能製造出來最大的差是4+3=7,最小的差是1+1=2
在37的倍數中,37、74、111、148、185、222、259中,只有185和60的倍數相差在7以內
由37×5-60×3=185-180=5=1+4=2+3
表示第一組的三位數和第二組的三位數只有一個數字是相同的,
可能的組合是A,B,E和C,D,E或是A,B,D和C,D,E,或是A,B,C和B,D,E
前兩組的D=180÷3=60、A=60+3=63
第三組的B=185÷3=61.....2非整數,不合
其中A-E=4,A-D=3,A-C=2,A-B=1
B-E=3,B-D=2,B-C=1
C-D=1
其次33=10+11+12≦任意三個兩位數和≦99+98+97=294
要滿足題意,第一組的三個兩位數和第二組的三個兩位數至少有一個數字,最多有2個數字是相同的
若有兩個數字是相同的,兩組數字和所能製造出來最大的差是4,最小的差是1
若有一個數字是相同的,兩組數字和所能製造出來最大的差是4+3=7,最小的差是1+1=2
在37的倍數中,37、74、111、148、185、222、259中,只有185和60的倍數相差在7以內
由37×5-60×3=185-180=5=1+4=2+3
表示第一組的三位數和第二組的三位數只有一個數字是相同的,
可能的組合是A,B,E和C,D,E或是A,B,D和C,D,E,或是A,B,C和B,D,E
前兩組的D=180÷3=60、A=60+3=63
第三組的B=185÷3=61.....2非整數,不合
-

J+W - 版 主

- 文章: 2162
- 註冊時間: 2003-12-30
[挑戰]已知一個正整數是N能被最小的十二個自然數(1~20)中的18個數整除
已知一個正整數是N能被最小的十二個自然數(1~20)中的18個數整除,而且那兩個不能整除N的數剛好是連續的自然數.請問這兩個不能整除N的數的和是多少??



∵24=16。 ∴16+17=33
完整的理由
假設2,3,5,7,11,13,17,19這些質數都能整除N的話
那麼不能整除N的連續整數只可能是8,9和,9,10或是14,15和15,16
8,9這組和N可以整除4和2矛盾;9,10這組和N可以整除5和2矛盾
14,15和15,16這兩組和N可以整除3和5矛盾
由以上的討論可以推知不能整除N的兩個連續整數必然是一個質數和一個含有單一質因數的高次方組合
唯一的可能只有16和17,16+17=33
此時最小的N值
-

J+W - 版 主

- 文章: 2162
- 註冊時間: 2003-12-30
第1頁(共1頁)



