題目為判斷級數 Σ[k:0->無窮大] [(k!k!)/(2k)!]4^k 為發散還收斂
我用ration test 出來的結果等於1,無法下結論。
還能用什麼檢驗法啊? 目前想到的是limit comparison test
但是我不確定能不能這樣用
因為:Sigma:[k:0->無窮大] [(k!k!)/(2k)!] 這個用ratio test判斷為收斂級數
然後用 comparison test ak=[(k!k!)/(2k)!]4^k , bk=[(k!k!)/(2k)!]
lim n->無窮大 [ak/bk] =lim n->無窮大 4^k 發散 ,所以 ak 發散
可是...我記得 comparison test lim n->無窮大 [ak/bk]=L 常數 然後ak隨著bk 發散收斂...
由我想法計算出來的L為發散,我可以直接判斷an為發散嗎?
[大學] 判斷級數收斂發散。

第1頁(共1頁)
Re: [大學] 判斷級數收斂發散。
徐瑋澤 寫到:題目為判斷級數 Σ[k:0->無窮大] [(k!k!)/(2k)!]4^k 為發散還收斂
我用ration test 出來的結果等於1,無法下結論。
還能用什麼檢驗法啊?
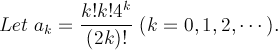
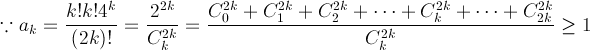
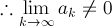
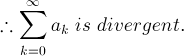
徐瑋澤 寫到:
目前想到的是limit comparison test
但是我不確定能不能這樣用
因為:Sigma:[k:0->無窮大] [(k!k!)/(2k)!] 這個用ratio test判斷為收斂級數
然後用 comparison test ak=[(k!k!)/(2k)!]4^k , bk=[(k!k!)/(2k)!]
lim n->無窮大 [ak/bk] =lim n->無窮大 4^k 發散 ,所以 ak 發散
可是...我記得 comparison test lim n->無窮大 [ak/bk]=L 常數 然後ak隨著bk 發散收斂...
由我想法計算出來的L為發散,我可以直接判斷an為發散嗎?
不行。舉例:令 ak=1/2k,bk=1/4k,
則 Σbk 為收斂,且 limk→∞ak/bk = ∞,但 Σak 為收斂而非發散。
-
benice - 專 家

- 文章: 269
- 註冊時間: 2010-02-08
第1頁(共1頁)
