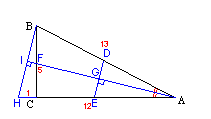
三角形ABC中,BC=5,AC=12,AB=13,在邊AB,AC上分別取D,E使線段DE將三角形ABC分成面積相等的兩部分,試求DE的最小長度。


??? 寫到:三角形ABC中,BC=5,AC=12,AB=13,在邊AB,AC上分別取D,E使線段DE將三角形ABC分成面積相等的兩部分,試求DE的最小長度。


 追求神乎其技,至高無上的數學境界!~
追求神乎其技,至高無上的數學境界!~ 

宇智波鼬 寫到:Another method:
We use coordinate Geometry.
Let A be the origin, C be (12,0), B be (12,5)
Also, D will be (12r,5r) E be (a,0) (Where r and a are both reals)
Obviously, 5ar=30, ar=6
The shortest distance is √[(12r-a)^2+25r^2]
=√(169r^2-144+36/r^2)
144 is a constant, so the value depends on 169r^2+36/r^2.
By the AM-GM, we can easily find out the minimum.
When r=6/13, 169r^2+36/r^2-144=12
So, DE=√12

